GALA CODES

Let’s understand activation functions with an exciting example. Consider the following dataset. We need to build a classification model for the following problem.

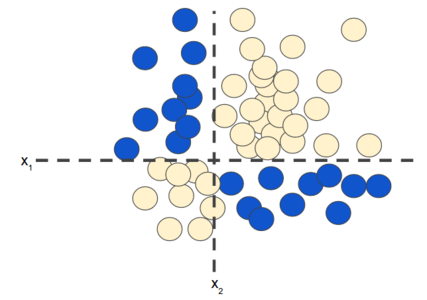
The above problem is a “non-linear” problem and we cannot predict a label using a model of the form

z = w1.x1 + w2.x2 + b

One possible solution to this problem is Feature Crosses. But what if we cannot even use Feature Crosses, like in the case of the problem given below,

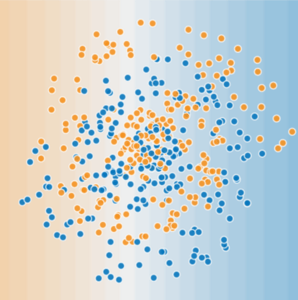
We know we can’t solve it using a linear model or Feature Crosses. Let’s see how Neural Networks might help here. Let’s take a simple neural network to solve this problem.

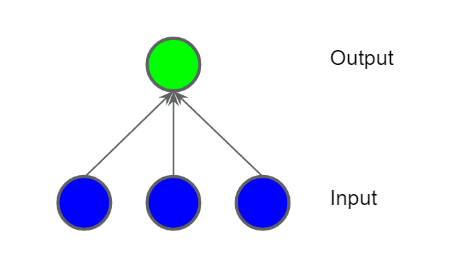
The blue circles are input features and the green ones are representing the weighted sum of the inputs. Let’s add a Hidden Layer (yellow) to this network to improve its ability to deal with non-linear problems.

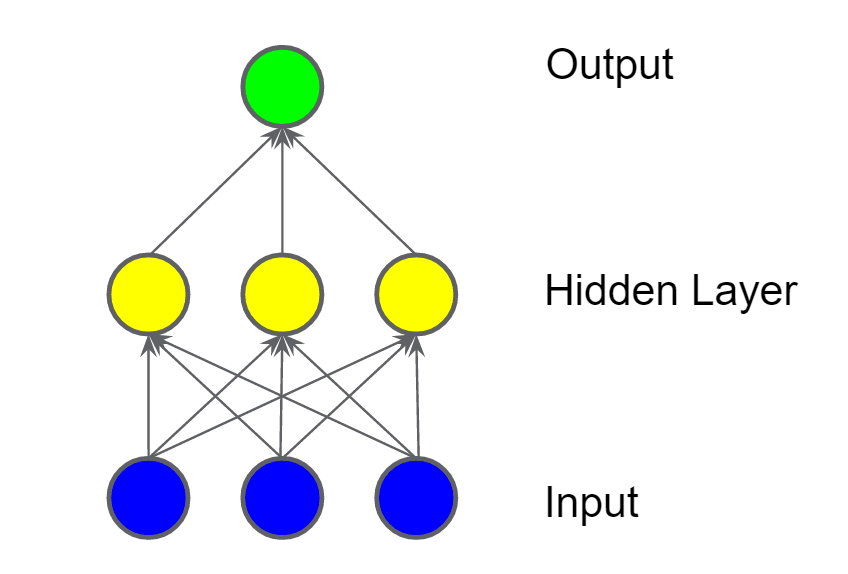
Will this model be able to solve our non-linearity issue? No. Will two of such hidden layers solve our non-linearity issues? Still No.

The output of linear models will always remain linear. So how do make it solve non-linear problems? The answer is, to use Activation Functions

Activation Functions

To model a nonlinear problem, we can directly introduce a nonlinearity. We can pipe each hidden layer node through a nonlinear function.

In the model represented by the following graph, the value of each node in Hidden Layer 1 is transformed by a nonlinear function before being passed on to the weighted sums of the next layer. This nonlinear function is called the activation function.

Adding layers has a greater impact now that we’ve included an activation function. Stacking non-linearities on top of non-linearities allows us to develop extremely complex relations between inputs and predicted outputs. In summary, each layer learns a more complicated, higher-level function from the raw inputs. Also check Chris Olah’s fantastic blog post for more intuition on how this works.

Common activation functions

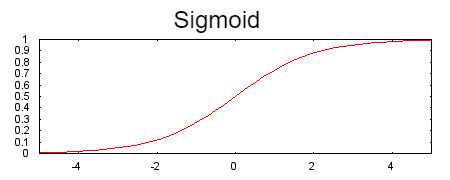
Sigmoid

The following sigmoid activation function converts the weighted sum to a value between 0 and 1

ReLU

Rectified Linear Unit often works a little better than a smooth function like the sigmoid while also being super easy to compute.

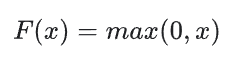
Any mathematical function can serve as an activation function. Suppose that σ represents our activation function (Relu, Sigmoid, or whatever). Consequently, the value of a node in the network is given by the following formula:

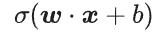
Summary

Now our model has all the standard components of what people usually mean when they say “neural networks”:

• A set of nodes, or neurons, organized in layers.
• A set of weights representing the connections between each layer and the layer beneath it. The layer beneath may be another layer or activation layer.
• A set of biases, one for each node.
• An activation function that transforms the output of each node in a layer. Different layers may have different activation functions.