GALA CODES

Logistic regression is used to calculate the probability of an outcome given an input variable. For e.g. probability of an email being spam or not spam. This model returns the probability of the outcome in a range of 0 to 1. We often use Logistic Regression combined with a threshold value in classification problems.

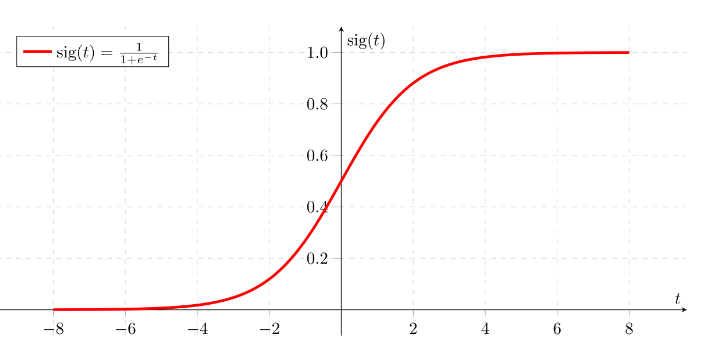
Logistic regression is a powerful supervised algorithm often used for binary classification. Logistic regression is essentially a Linear Regression Model with a Logistic function. The logistic regression model computes a sum of the input features (in most cases, there is a bias term), and calculates the logistic of the result. Then the logistic function bounds the value of the output in the range 0 to 1, thus, it comes in handy in problems with probabilities.

Let us consider a Logistic regression model to calculate the probability of a mail being spam

Output = 0 or 1

Hypothesis => z = w.x + b

hΘ(x) = sigmoid (Z)

Sigmoid Function

Types of Logistic Regression

1. Binary

There are only 2 categories whose probabilities are needed. E.g. spam or not spam

2. Multinomial

Three or more categories can exist but with no specific ordering. E.g. Veg, Non-veg and Vegan.

3. Ordinal

Three or more categories with specific ordering. E.g. Movie rating from 1 to 5

Loss Function

We know that in Linear Regression, we use Mean Squared Error (MSE) to compute the loss. However, we use the Log Loss function in Logistic Regression.

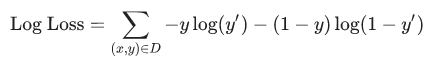
Regularization

Regularization is extremely important in Logistic Regression. Without regularization, the asymptotic nature of the Logistic regression would keep driving loss towards 0 in higher dimensions. Without a regularization function, the model will be completely overfitted and reach infinite size weights for every example. This can happen in high dimensional data with feature crosses when there is a huge mass or rare crosses that happen only on one example each.

We can use L2 regularization to overcome this issue.