GALA CODES

In machine learning, a common problem is models overfitting to the training data and thus not generalizing on test data. Regularization is a technique to tackle this problem of overfitting by penalizing bad weights or reducing coefficients toward the value of zero.

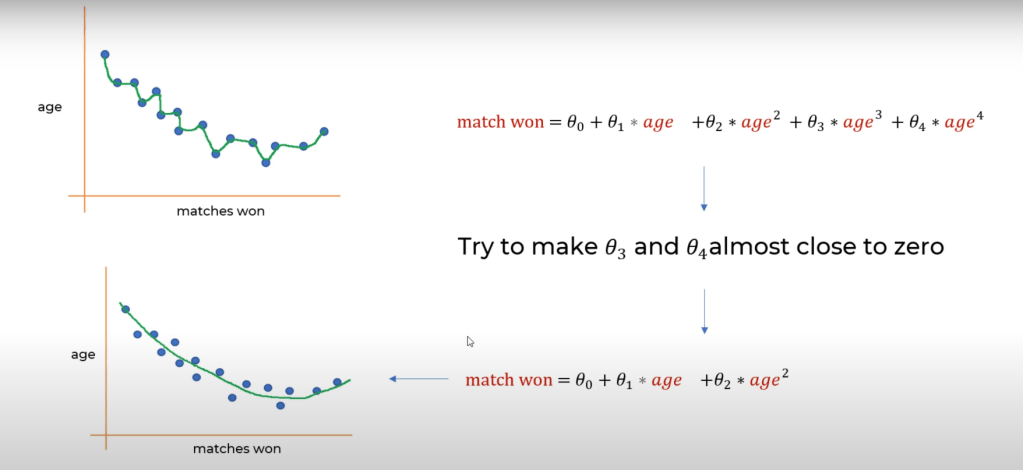
L1 regularization

L1 regularization is also known as Ridge regularization. The idea is to add another parameter, λ, at the end of the equation of the model. This lambda is a free parameter that we can control and change to see what works better. Lambda is followed by the absolute value of θ. What this means is that whenever a higher value of θ is chosen, it will increase the value of MSE and thus penalize the model. This will help in keeping the overfitting in check as the complexity of the model will come down.

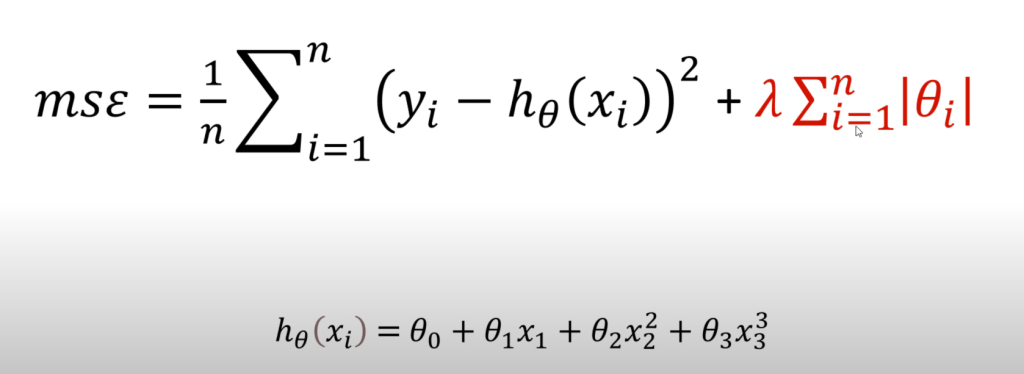
L2 regularization

L2 regularization is also known as Lasso regularization. The lambda is a free parameter that we can control and change to see what works better just as in the case of Ridge Regularization. Lambda is followed by the squared value of θ. This makes sure that the model is penalized by a very high value when choosing a higher θ (parameter) value and by a very small value when choosing a smaller parameter value (say 0 to 1). L2 is more popular and used in most places.

It has the following effects on a model:

• L2 encourages the weight values toward zero (not exactly 0)
• Encourages the mean of the weights toward 0, with a normal (bell-shaped or Gaussian) distribution.

Sci-Kit learn has pre-defined functions for Ridge and Lasso.

Lambda

Developers can tune the overall impact of the regularization term by multiplying its value with a scalar known as Lambda (aka. Regularization rate)

Increasing the Lambda value strengthens the regularization. However, choosing the right lambda value is important.

• A very high regularization rate will penalize the model even at low complexity and thus exposes it to a risk of underfitting the data.
• A very low value will not be able to reduce the complexity of the model and it may start overfitting.

The ideal value for Lambda is the one that helps the model generalize on unseen data. This can be done by some fine-tuning and trying multiple values manually. The regularization rate is somewhat similar to the learning rate. The key is to maintain a perfect balance between not too low and not too high.